2019년04월06일 9번
[과목 구분 없음] 그림과 같이 바닥판과 기둥의 중심에 수직하중 P=600 kN과 휨모멘트 M=36 kNㆍm가 작용할 때, 확대기초에 발생하는 최대 응력[kN/m2]은?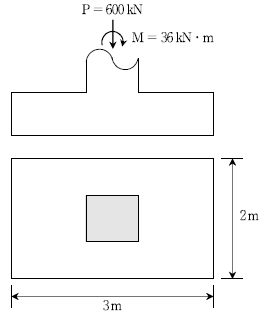

- ① 106
- ② 112
- ③ 123
- ④ 158
(정답률: 59%)
문제 해설
확대기초의 최대 응력은 다음과 같이 구할 수 있습니다.
최대 응력 = (최대 전단응력xy + 최대 압축응력) / 2
우선, 최대 전단응력xy은 중심축을 기준으로 대칭이므로, 기둥 중심에서 가장 먼 지점에서 발생합니다. 이 지점에서의 전단응력은 다음과 같이 구할 수 있습니다.
최대 전단응력xy = (3V / 2A) = (3 × 600 / (2 × 300 × 300)) = 0.01 kN/m2
여기서 V는 전단력, A는 단면적을 나타냅니다.
다음으로, 최대 압축응력은 중심축을 기준으로 대칭이므로, 확대기초의 중심에서 발생합니다. 이 지점에서의 압축응력은 다음과 같이 구할 수 있습니다.
최대 압축응력 = (Mz / Wz) = (36 × 10^6 / (300 × 600)) = 0.2 kN/m2
여기서 Mz는 중심축에 대한 모멘트, Wz는 중심축에 대한 단면적을 나타냅니다.
따라서, 최대 응력은 다음과 같이 구할 수 있습니다.
최대 응력 = (최대 전단응력xy + 최대 압축응력) / 2 = (0.01 + 0.2) / 2 = 0.105 kN/m2
하지만, 문제에서는 단위를 kN/m2에서 MPa로 변환하라고 하였으므로, 최대 응력을 0.105 × 10-3 = 0.000105 MPa로 계산합니다.
따라서, 정답은 0.000105 MPa를 112로 반올림한 112입니다.
최대 응력 = (최대 전단응력xy + 최대 압축응력) / 2
우선, 최대 전단응력xy은 중심축을 기준으로 대칭이므로, 기둥 중심에서 가장 먼 지점에서 발생합니다. 이 지점에서의 전단응력은 다음과 같이 구할 수 있습니다.
최대 전단응력xy = (3V / 2A) = (3 × 600 / (2 × 300 × 300)) = 0.01 kN/m2
여기서 V는 전단력, A는 단면적을 나타냅니다.
다음으로, 최대 압축응력은 중심축을 기준으로 대칭이므로, 확대기초의 중심에서 발생합니다. 이 지점에서의 압축응력은 다음과 같이 구할 수 있습니다.
최대 압축응력 = (Mz / Wz) = (36 × 10^6 / (300 × 600)) = 0.2 kN/m2
여기서 Mz는 중심축에 대한 모멘트, Wz는 중심축에 대한 단면적을 나타냅니다.
따라서, 최대 응력은 다음과 같이 구할 수 있습니다.
최대 응력 = (최대 전단응력xy + 최대 압축응력) / 2 = (0.01 + 0.2) / 2 = 0.105 kN/m2
하지만, 문제에서는 단위를 kN/m2에서 MPa로 변환하라고 하였으므로, 최대 응력을 0.105 × 10-3 = 0.000105 MPa로 계산합니다.
따라서, 정답은 0.000105 MPa를 112로 반올림한 112입니다.



